Streuungsmaße, auch als Dispersionsparameter bekannt, liefern Informationen über die Verteilung und Variabilität der Werte eines Merkmals in einem Datensatz. Sie zeigen, wie weit die einzelnen Werte um den Mittelwert streuen und helfen dabei, die Datenverteilung zu beschreiben.
Es handelt sich um die Variabilität der Merkmalsausprägungen. Beide Maße setzen theoretisch ein metrisches Skalenniveau voraus.

Je nach Merkmalstyp werden unterschiedliche Skalenniveaus unterschieden: Nominal-, Ordinal-, Intervall- und Ratioskala.
1a: Varianz
Die Varianz (s², englisch "variance") berechnet sich als durchschnittliche quadratische Abweichung der einzelnen Messwerte vom arithmetischen Mittelwert:
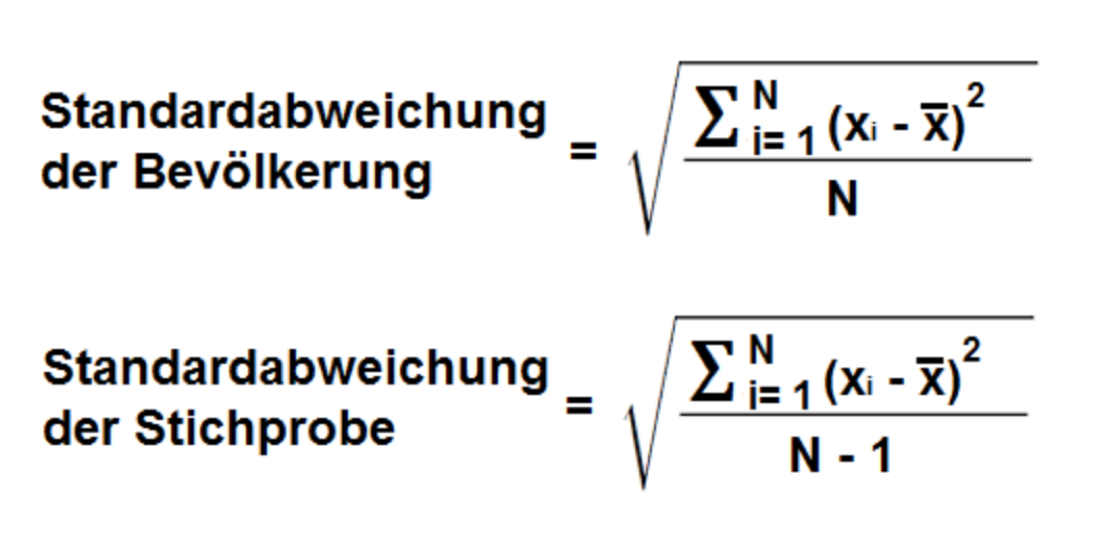
x1 = 4, x2 = 7, x3 = 1, x4 = 9 -> Mittelwert: 5,25
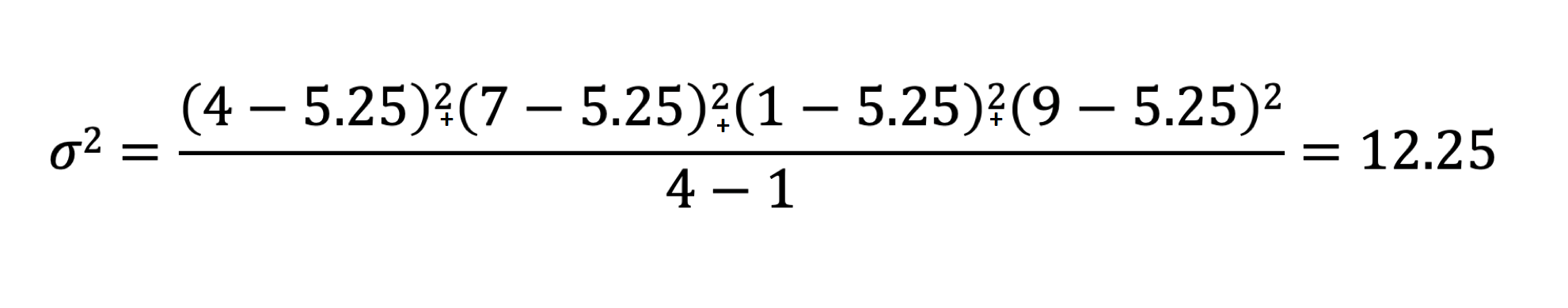
1b: Standardabweichung
Die Standardabweichung (s, englisch "standard deviation" oder kurz "SD") ist die Quadratwurzel der Varianz. Im obigen Beispiel wird die Standardabweichung wie folgt berechnet:
Im Gegensatz zur Varianz hat die Standardabweichung den Vorteil, dass sie in derselben Einheit wie die ursprünglichen Messwerte angegeben wird, was die Interpretation erleichtert. Anstatt beispielsweise von schwer verständlichen "Quadratstunden" zu sprechen, wenn die Varianz 12,25 beträgt, zeigt die Standardabweichung anschaulich, dass die Werte im Durchschnitt um etwa 3,5 Stunden vom Mittelwert abweichen – was wesentlich intuitiver ist.
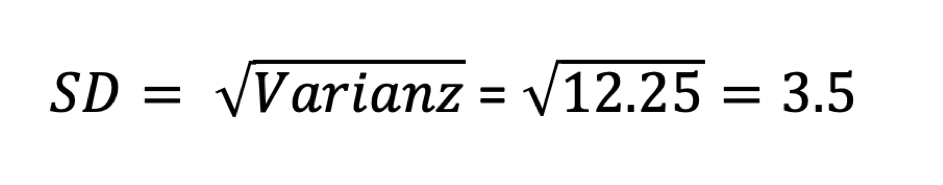
Sowohl bei der Varianz als auch bei der Standardabweichung haben Ausreißer einen großen Einfluss. Daher ist es wichtig, die Datenverteilung vor der Berechnung von Kennwerten oder statistischen Tests zu überprüfen.
2a: Schiefe
Die Schiefe (englisch "skewness") quantifiziert die Asymmetrie einer Häufigkeitsverteilung. Anhand der Lage von Mittelwert, Median und Modus zueinander lässt sich häufig feststellen, ob und in welche Richtung eine Verteilung im Vergleich zur Normalverteilung schief ist.

2b: Steilheit
Die Kurtosis (auch Wölbung, Steilheit oder Exzess genannt, englisch "kurtosis") beschreibt, ob eine Verteilung im Vergleich zur Normalverteilung eher spitzgipflig (leptokurtisch) oder flachgipflig (platykurtisch) ist.





