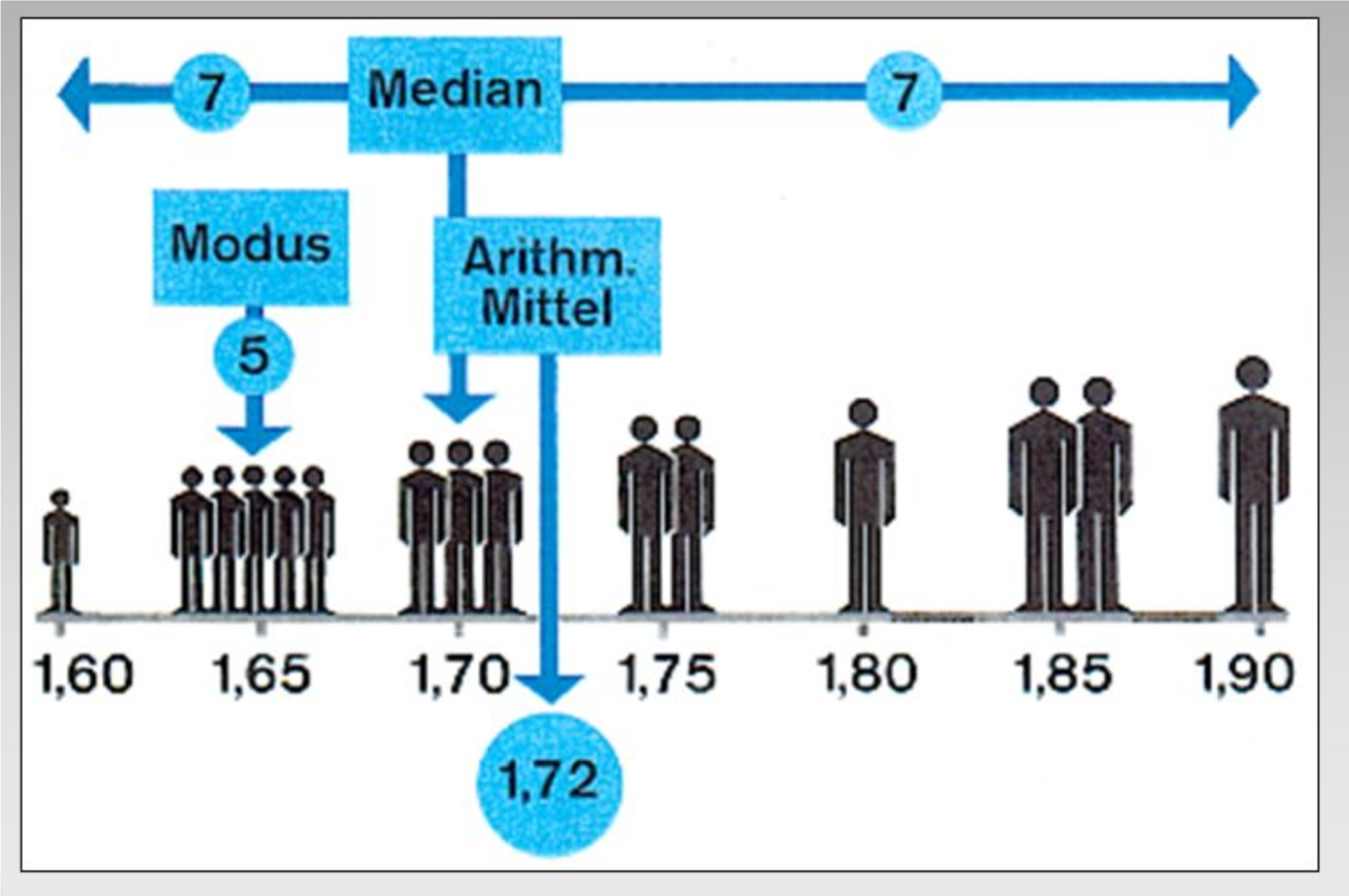
Lagemasse, auch als zentrale Tendenz bekannt, beschreiben die Häufigkeitsverteilung durch einen einzelnen Wert, der die gesamte Verteilung bestmöglich repräsentiert. Wichtige Kennzahlen sind das arithmetische Mittel, der Median und der Modus.
Das Skalenniveau der Daten sollte bei der Berechnung der Lagemasse unbedingt beachtet werden.
Abhängig von der Art des Merkmals werden verschiedene Skalenniveaus unterschieden: Nominal-, Ordinal-, Intervall- und Ratioskala.
Arithmetisches Mittel
Das arithmetische Mittel, auch als Mittelwert oder "mean" bekannt, ist das am häufigsten verwendete Maß für die zentrale Tendenz. Es entspricht dem mathematischen Durchschnitt. Hier ein Beispiel zur Berechnung:
x1 = 5; x2 = 4; x3 = 3
x̄ = (5 + 4 + 3) / 3 = 4
Median
Der Median, auch als Zentralwert oder "median" bezeichnet, teilt die Stichprobe in zwei gleich große Hälften. Es handelt sich um das 50%-Quantil der Verteilung einer Variablen. Es gibt genauso viele Werte unterhalb wie oberhalb dieses Wertes. Voraussetzung ist mindestens ein ordinales Skalenniveau.
Beispiel 1
Bestimme den Median dieser Werte:
1, 4, 2, 5, 0
Zuerst ordnen wir die Werte: 0, 1, 2, 4, 5
Es liegt eine ungerade Anzahl an Werten vor, also ist der Median der Punkt in der Mitte der Daten:
0, 1, 2, 4, 5
Der Median ist 2.
Beispiel 2
Bestimme den Median dieser Werte:
10, 40, 20, 60
Zuerst ordnen wir die Werte: 10, 20, 40, 60
Es liegt eine gerade Anzahl an Werten vor, also ist der Median gleich dem arithmetischen Mittel der beiden mittleren Werte:
Median = (20 + 40) / 2 = 30
Der Median ist 30.
Modus
Der Modus, auch Modalwert oder "mode" genannt, ist der am häufigsten vorkommende Wert in einer Verteilung. Er wird insbesondere bei nominalskalierten Daten genutzt, zum Beispiel zur Bestimmung der häufigsten Hunderasse. Wenn mehrere Ausprägungen gleich häufig auftreten, ist der Modus nicht eindeutig; beide Ausprägungen werden dann als Modi bezeichnet, und die Verteilung ist bimodal. Bei kleinen Stichproben kann der Modalwert stark von Zufallsschwankungen beeinflusst sein.
Beispiel 1
0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3
Der Modus ist 1.
Beispiel 2
0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4
Die Modi sind 1 und 2.

